大学受験数学のおすすめ参考書 志望別・良問問題集の選び方

数学は、「実際に問題を解くこと」が重要な教科です。そういう意味でも、自分に合った問題集や参考書を選ぶことは、入試の合否に直結すると言っても過言ではありません。自分に最適な問題集・参考書の選び方について解説します。

高校の数学はここが違う！

高校の数学は中学の数学とは大きく異なります。学習する内容が多いことに加え、それぞれの単元の内容が圧倒的に難しくなります。受験にむけて効率的に進めるためにも、まずは高校数学の全体像を把握することから始めましょう。

高校1年の必修科目　数Ⅰ＋Aから始まる

高校1年で学ぶ「数学Ⅰ＋A」。文科省が定めた必修科目である数学Ⅰはもちろん、数学Aもほとんどの学校で必修となっており、避けては通れない科目です。

中でも数学Ⅰは、数学Ⅱなどの今後の数学につながる内容が多く、さらに物理とも関わりがある内容まで含んでいます。様々な科目の基礎となるため、非常に重要な科目なのです。

数学Ⅰの内容は「数と式」「二次関数」「図形と計量」「データの分析」の4つに分かれています。特に二次関数と図形と計量は、入試にも頻出であり、これからの学習の柱となる超重要単元です。高校1年の長期休みごとに復習することをおすすめします。

数学Aでは、「場合の数と確率」「図形の性質」「数学と人間の活動」の3つの単元を扱います。数学Aは数学Bなど他の科目への影響は限定的ですが、大学入試では頻出であり、後回しにすると後々苦労することも少なくありません。特に数学Aで扱う単元は、得意・不得意の個人差が出やすいものが多いです。独学では対策が難しいので、苦手意識が芽生えたら、早めに先生や友人、塾などに相談して対策をとりましょう。

高校2年　数Ⅱ＋Bの範囲

高校2年で学ぶ「数学Ⅱ＋B」。看護系や文系の一部の大学など、数学Ⅱ＋Bが不要な大学もありますが、そこまで多くありません。受験校の選択肢を狭めないためにも、ほとんどの受験生にとって数学Ⅱ＋Bは避けることのできない科目です。

数学Ⅱの内容は、「いろいろな式」「図形と方程式」「指数関数・対数関数」「三角関数」「微分・積分の考え」の5単元です。どの単元も数学Ⅰに比べ、暗記すべき公式や計算量がかなり増えるため、習得にはかなりの演習量が求められます。特に、理系志望の人は数学Ⅲ＋Cに大きく影響するので、高校2年のうちに完成度を高めておきたいです。もし理解につまずいた場合は、数学Ⅰの戻り学習が効果的です。

数学Bでは「数列」と「統計的な推測」を学びます。特に「数列」は、大学入試はもちろん数学Ⅲにも影響する重要単元です。知っておかないと難しい解法が多くあるため、とにかくたくさんの問題演習を行いパターンに慣れることが必要です。一方で、統計的な推測は共通テストの選択問題で出題されるため、それなりに重要なのですが他の単元との関連が薄いです。高校2年のうちは数列を優先して復習しましょう。

高校3年　数Ⅲ＋Cの範囲

高校3年で学ぶ「数学Ⅲ＋C」。理系の大学受験において、多くの大学で必須となるうえ、数学Cのベクトルは文系の大学でも出題されます。ほとんどの理系受験生にとって避けることのできない科目というだけではなく、文系の受験生にとっても無関係ではない科目です。

数学Ⅲでは、「極限」「微分」「積分」の3つの単元を学びます。どの単元も数学Ⅰ+A、②+Ｂと比べ物にならないくらい計算量が多く、教科書レベルの問題でも難易度が高いのが特徴です。特に積分は、理系の大学で必ずと言って良いほど出題される、受験生にとって最重要単元です。覚えなくてはいけない計算パターンがたくさんあるため、とにかくたくさんの問題演習を行う必要があります。また、学校によっては、数学Ⅲを学び終えてから入試までの期間があまりないこともあります。その場合は、できる限り習っている間に完成度を上げたいところです。

数学Cの内容は「ベクトル」「平面上の曲線と複素数平面」の２単元です。特に、ベクトルは、高校3年ではなく高校2年で数学Bとともに学ぶことが多い重要単元です。ただ公式を覚えるだけでは解けるようにならず、図形的な意味や使える場面まで理解する必要があります。

文系、理系　志望が明確になったら、入試科目と目指すレベルを確認する

大学や学部の志望が決まったら、「入試科目」と「レベル」を確認しましょう。必要な科目やレベルによって、受験に向けた参考書や問題集の選び方が異なります。

理系の学部の大部分は数学Ⅲ＋Cが入試科目になりますが、獣医学部や薬学部など数学Ⅲ＋Cを課さない入試もあります。文系の大学でも注意が必要です。私立文系であれば数学が不要なイメージがあるかもしれませんが、近年では私立文系大学での数学入試が少なくありません。数学で受験したほうが、倍率が低いこともあるため、数学入試を検討する価値は十分あるのです。理系、文系という分類だけで、数学をどこまで学ぶか決めるのではなく、志望大学の入試科目を調べたうえで判断しましょう。

また、志望大学の入試問題の「レベル」を知ることも重要です。問題の難易度や出題傾向によって、選ぶべき参考書や問題集の選び方や使用時期などが変わってきます。

例えば東京大学であれば、全問が記述式の難問で、試験時間内に完答することが大変難しいです。記述に慣れることに加え、捨て問を見極める練習を行うため、高校3年の大部分を過去問演習に充てることが理想です。逆算すると、高校2年生までに『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』、『ハイレベル数学Ⅲ・Ｃ［平面上の曲線と複素数平面］の完全攻略〈改訂版〉』のような入試標準～やや難レベルの問題集を終わらせる必要があるのです。

他にも慶應義塾大学の経済学部であれば、マーク式と記述式が半々で出題されることと、制限時間が厳しいことが特徴です。問題形式や時間制限への慣れは重要ですが、難易度をふまえると高校３年生の秋ごろから過去問演習を始めれば十分間に合います。つまり、『数学Ⅰ・A　基本問題演習』、『数学II・B　基本問題演習』のような入試標準レベルの問題集を高校3年生の夏までに完璧にすれば良いことになるのです。

高校数学の参考書の選び方

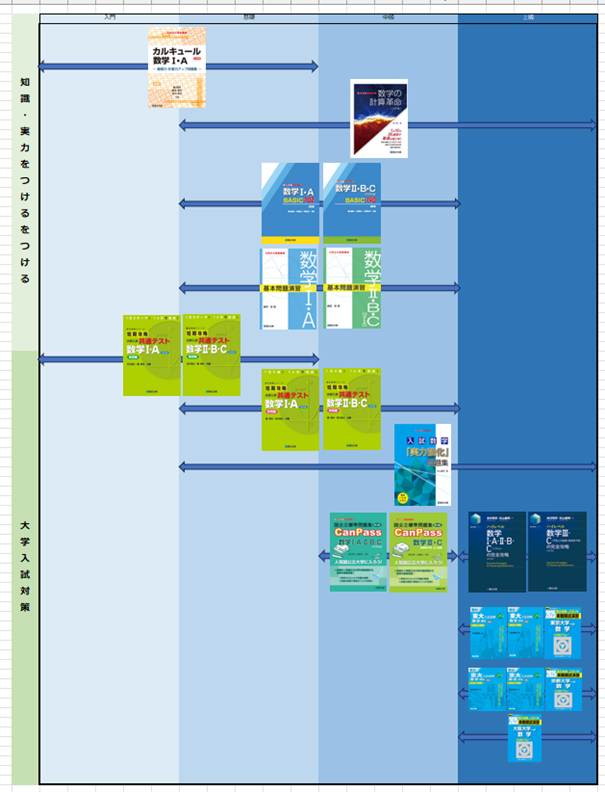
駿台文庫　数学参考書

では志望校合格に向けた、参考書はどのように選べばいいでしょうか？

理解を深めるために　わかりやすい参考書を選ぶ

大学受験を見据えて学習を進めるうえで、自分にとってわかりやすい参考書を選ぶことはとても重要です。わかりやすい参考書を選ぶためのポイントは、参考書の「目的」と「レベル」、「文体や構成」の3つが自分に合っているかどうかです。

参考書には、学校授業の予習復習を目的にしたものと、受験勉強を目的にしたものがあります。前者は初めて学ぶ人向けに用語や概念の解説を丁寧に行っているものが多く、後者は既習の生徒向けに実戦的な解法を中心に解説しているものが多いです。このように内容がかなり変わってくるので、目的に合ったものを選びましょう。

また、受験勉強を目的にした参考書は、対象とするレベルによって難易度が大きく異なります。難しすぎる参考書は学習効率も良くないですし、モチベーションの低下にもつながります。内容に目を通して、解説を読んで理解できるレベルかどうかチェックしておきましょう。

最後に、参考書の文体や構成も重要です。例えば、講義形式でカジュアルな言葉遣いで書かれている参考書もあれば、数学らしい簡潔な表現で書かれている参考書もあります。他にも、図やグラフ、解説の量など参考書によってさまざまです。特に解答解説は人によって「合う」「合わない」があるため、実際に目を通して、自分にとって理解しやすいと感じるものを選びましょう。

基礎を固める網羅系　苦手な単元を克服する単元系

受験勉強を目的とした参考書の中には、大きく分けて「網羅系」と「単元系」の2種類があると思います。

網羅系の参考書とは、入試に必要な解法を辞書のように網羅的に扱っている参考書のことです。主な目的は解法のインプットなので、必ずしも初見で解ける必要はなく解答解説を読んで、理解できれば問題ありません。網羅形の参考書は分量が多いので、高1や高2の早い時期から計画的に取り組み、受験生になる前に基本的な公式や解法をマスターしておきます。例えば、数学が得意な人におすすめなのが『入試数学「実力強化」問題集』です。入試に必要な知識をほぼすべて習得できますし、それだけではなく入試にも直結する難易度の高い問題にも同時に挑戦することができます。

一方、単元系の参考書とは、「ベクトル」や「平面上の曲線」など特定単元に絞った内容を扱っている参考書のことです。単元が絞られているため一冊の量が比較的少なく、短期間で終わらせやすいメリットがあります。模試で苦手な範囲が判明したときや、短期間で苦手な単元を克服する際に活用しましょう。なお、網羅系参考書でも単元を絞って取り組めば、単元系のような使い方が可能です。

良問を数多くこなすための問題集

参考書の目的がまず基本的な解法を学ぶことであるのに対し、大学入試対策の問題集の目的は、身につけた解法を適切に使う訓練をすることです。参考書ではまず基本的な型を身につけることを目的としたシンプルな問題がメインであるのに対し、実際の大学入試では、表現や出題形式が複雑で多岐に渡ります。大学入試に対応するためには、この複雑な出題に対して、問題の構造を見抜き、基本の解法を組み合わせる力が必要なのです。

そこで大切なのが1問から多くを学べる質の高い問題、つまり良問が多く収録された問題集を選ぶことです。また、良問から深く学ぶために、解説の質・量が重要です。良問の解説はその一問の解き方を説明するだけではなく、周辺知識や他の問題への応用のさせ方などまで載っていることが多いものです。

『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』『ハイレベル数学Ⅲ・Ｃ［平面上の曲線と複素数平面］の完全攻略〈改訂版〉』は厳選された40問程度が載っており、1問に対して解説がおよそ5ページと非常に充実しています。難関大を目指す人の仕上げの一冊としておすすめです。

問題集は難易度のレベル感で選ぶ

問題集を選ぶときは、良問が収録されているかどうかと同じくらい「レベル」が自分に合っているかが大切です。背伸びして難しい問題集に手を出したくなる気持ちはわかりますが、難しすぎる問題集はかえって非効率です。問題集の難易度は「過ぎたるは猶及ばざるが如し」。自分のレベルや目的にあった問題集を選びましょう。

例えば、数学Ⅱ+Bに入る前に短期間で数学Ⅰ＋Aの復習をしたい場合、いきなり受験基礎レベルの問題集は難し過ぎます。数学Ⅱ＋Bの準備には、『カルキュール数学Ⅰ・Ａ［基礎力・計算力アップ問題集］〈三訂版〉』のような、基本に絞った薄めの問題集が適しています。1単元あたり見開き3,4ページと、無理なく学校の授業と並行して進められる量なので、日々の復習にもおすすめです。

一方、受験に向けた復習をしたい高校1,2年生には、『数学Ⅰ・A　BASIC 102〈改訂版〉』『数学II・B・C［ベクトル］BASIC 140〈改訂版〉』のような、受験基礎レベル問題集がおすすめです。名前の通り、Ⅰ+ Aは102問、Ⅱ＋Bは140問と同じレベルの問題集と比較しても問題数が絞り込まれており、長期休みなどに一気に終わらせることも可能です。

また、ある程度単元の復習ができていて、入試標準レベルの入試演習を始めたい高校2,3年生には、『数学Ⅰ・A　基本問題演習』『数学Ⅱ・Ｂ・Ｃ［ベクトル］ 基本問題演習』といった実戦的な問題集が良いでしょう。目標時間が書いてあったり、別解や考え方など解説が豊富だったりと、取り組みやすい工夫が凝らされています。

出題形式に慣れるため問題集

問題集を解く目的は、当然学力を伸ばすためですが、それだけではありません。試験本番の出題形式に慣れることも、問題集の重要な目的のひとつです。

大学入学共通テスト（以下、共通テスト）は、本文を穴埋めする形で、誘導に乗りながら問題を解く必要があります。また、文章量が非常に多く、制限時間内に解き切るのは至難の業です。得点を伸ばすためには数学の学力はもちろん、形式への慣れも重要なのです。そこで役立つのが、『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 実戦編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 実戦編〈改訂版〉』のような、共通テストに特化した問題集です。大問毎に目標時間が定められており、演習を繰り返すことで自然と適切な時間配分ができるようになります。

また、国公立大学の二次試験には、記述が重視され、私立大学と比較して証明問題の出題が多いという特徴があります。記述答案の作り方を学べる解説の詳しい問題集を使うのが、対策には一番です。『国公立標準問題集 CanPass数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］〈第３版〉』や『国公立標準問題集 CanPass数学Ⅲ・Ｃ［複素数平面、式と曲線］〈第３版〉』のように、実際の国公立大学の過去問を収録し、記述答案を作るための詳しい解説がついた問題集がおすすめです。         

共通テスト対策のための数学の参考書・問題集

共通テストは国公立大学はもちろん、私立大学の入試にも使用されることが少なくありません。また、近年では文系の大学でも数学の共通テストの受験を必須にするなど、数学の共通テスト対策は多くの受験生にとって対策が必須のものになっています。

出題範囲を把握する

共通テスト対策を行う前に、まずは大問構成と出題範囲を正しく把握しましょう。

数学Ⅰ＋Aは4つの大問で構成されており、「数学と人間の活動」以外の数学Ⅰ＋Aのすべての単元から幅広く出題されます。中でも「データの分析」は、個別学力試験ではほとんど出題されないため、共通テストにあわせて対策を進めたい単元です。共通テスト模試の直前や、長期休みなどのタイミングで復習しておくと良いでしょう。

数学Ⅱ＋B＋Cは7つの大問で構成されており、大問1〜3は数学Ⅱからの出題で、すべて必答です。一方で大問4〜7は、数学Bの「数列」「統計的な推測」と数学Cの「ベクトル」「平面上の曲線と複素数平面」から出題されており、4問中3問選択します。どの問題を選択するかは、概ね文系理系で決まります。理系は、「数列」「ベクトル」「平面上の曲線と複素数平面」を選択することが多いです。「統計的な推測」は数学Ⅰのデータの分析同様、個別学力試験での出題がほとんどないためです。ただ、「平面上の曲線と複素数平面」は理系入試で出題される単元のため、文系の人は学習していないことが多いため「数列」「統計的な推測」「ベクトル」を選択する人が大半でしょう。

出題範囲を把握したら、どの参考書・問題集を使って対策するか決めましょう。最も効率よく共通テストの点数を上げる方法は、すべての大問から満遍なく得点することです。

単元の知識に不安がある場合は、『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 基礎編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 基礎編〈改訂版〉』などの共通テストに必要な知識に絞って効率よく復習できる参考書や問題集を使用しましょう。単元の知識に問題がなければ、『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 実戦編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 実戦編〈改訂版〉』のような共通テスト形式の問題集を用いて、問題形式や時間配分に慣れましょう。問題形式にある程度慣れた人は、最後に過去問などを用いて、大問を解く順番や大問ごとの解く順番など、より本番に近い形で演習を積めば対策としては十分です。

医学部志望のおすすめ数学参考書

医学部受験は、他の学部と比べものにならないほどスピードと正確性が求められます。制限時間が厳しい試験なうえに、合格ラインにかなりの人数が集まる１点を争う勝負になるからです。

このような厳しい戦いに対応するためには、早期に数学の完成度を高めておくことが大切です。特に国公立志望の場合は、まず共通テストを突破しなければなりません。国公立医学部の場合、共通テストで8割以上の得点が求められますが、これを高2のうちにクリアしておくことを1つの目安にするのがよいでしょう。高2のうちに『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 実戦編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 実戦編〈改訂版〉』などに取り組み、共通テスト対策を早期に終えることで、個別試験対策に十分な時間を割くことが可能になります。

二次試験対策は旧帝大などの難関大を除けば、入試標準レベルの出題が中心です。網羅系の参考書を高校2年までに終わらせたうえで、最終的に『国公立標準問題集 CanPass数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］〈第３版〉』や『国公立標準問題集 CanPass数学Ⅲ・Ｃ［複素数平面、式と曲線］〈第３版〉』などの国公立大学の標準問題を多く収録した問題集を仕上げれば良いでしょう。

私立医学部の場合は、大学ごとに難易度や時間制限の厳しさが大きく異なります。基本的な学力は、『数学Ⅰ・A　基本問題演習』『数学Ⅱ・Ｂ・Ｃ［ベクトル］ 基本問題演習』などの入試標準レベルの問題集で十分な大学も多いですが、志望校の出題傾向を把握したうえで対策することが重要です。例えば、東邦大学は試験時間90分に対して、大問が10問出題される非常に時間制限が厳しい試験です。日々の演習で、易しい問題を見極めてから解くなど優先順位をつける練習をしておくと良いでしょう。

志望校別おすすめ参考書

個別学力試験の傾向は、大学によって大きく異なります。大学別に特化した対策なしに合格するのは極めて難しいものです。ここでは、大学の個別学力試験の対策と、おすすめの参考書を紹介します。

東京大学志望のおすすめ数学参考書

東大数学の特徴は、難易度の高さと時間制限の厳しさです。全問が記述式の難問で、試験時間内に完答することはほぼ不可能です。また、共通テストも8割程度得点しないと、二次試験を受験することすらできないため、共通テストの対策も必須です。

共通テスト対策としては、高2のうちに8割以上得点することを目標とすると良いでしょう。高2のうちに『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 実戦編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 実戦編〈改訂版〉』などに取り組み、共通テスト対策を早期に終えて、過去問演習に時間を割くようにします。

二次試験対策としては、記述に慣れることに加え、問題の難易度を見極め、優先順位をつける練習が求められるため、高3の大部分を過去問演習に充てるのが理想です。逆算すると、高2までに『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』、『ハイレベル数学Ⅲ・Ｃ［平面上の曲線と複素数平面］の完全攻略〈改訂版〉』のような入試標準～やや難レベルの問題集を終わらせる必要があります。過去問には、単元で問題を分けているものもありますが、『東大入試詳解25年 数学〈理科〉〈第3版〉』『東大入試詳解25年 数学〈文科〉〈第3版〉』のように問題を年度ごとに分けているものの方が実践的でおすすめです。

京都大学志望のおすすめ数学参考書

京大数学の特徴は、シンプルな問題設定です。誘導のない問題も多く、自分で解法の筋道を論理的に考え、記述する力が求められます。東大と比べると、計算の複雑さや制限時間の厳しさは控えめですが、その分、論理的な思考力の重要度が高いです。

対策としては、高3の夏までに入試標準～やや難レベルの問題集を一通り終わらせるのが良いでしょう。『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』、『ハイレベル数学Ⅲ・Ｃ［平面上の曲線と複素数平面］の完全攻略〈改訂版〉』は、解答に至るまでの思考のプロセスや他の問題への応用の仕方が詳しく載っており、解答解説を読み込むことで、京大数学に必要な論理的思考力を養うことができます。過去問は高3の夏から取り組むのがおすすめです。誘導のない出題や記述に慣れるため、早めに過去問に取り組むことが理想です。

また、共通テストの対策も重要です。難関大に共通する目標ですが、高2の時点で7,8割を目指して対策しておきましょう。高2のうちに『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 実戦編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 実戦編〈改訂版〉』を終わらせることを目指してください。

東京科学大学志望のおすすめ数学参考書

東京科学大数学の特徴は、計算の複雑さです。大問５つに対して３時間と試験時間は比較的長く、スピードよりも、複雑な計算を正確に行う力が求められます。

数Ⅲの極限、微分、積分、そして数Aの整数、場合の数、確率と頻出単元がはっきりしていることも特徴です。出題傾向を掴むために、高3の夏から半年ほど過去問演習に時間を割きましょう。夏までに、『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』、『ハイレベル数学Ⅲ・Ｃ［平面上の曲線と複素数平面］の完全攻略〈改訂版〉』などの入試標準～やや難レベルの問題集を終わらせておくのがおすすめです。

なお、共通テストの得点は、二次試験に進めるかどうかの判定にのみ使用されます。６割強得点できればあとは二次試験勝負なので、特別な対策は不要です。東京科学大学レベルの数学に対応できれば、共通テストは特別な対策をせずとも十分得点できるはずです。

※ 試験時間や共通テストの配点は変更される可能性があります。

旧帝大志望のおすすめ数学参考書

東京大学・京都大学以外の旧帝大を目指す場合、大学によって出題傾向や難易度が異なるので志望校に合わせた対策を行う必要があります。

例えば、北海道大学は標準レベルかつ計算力が必要な問題が出題されます。計算力に不安がある人は計算問題集を併用しつつ、国公立大学の標準レベルの問題を多く収録した『国公立標準問題集 CanPass数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］〈第３版〉』『国公立標準問題集 CanPass数学Ⅲ・Ｃ［複素数平面、式と曲線］〈第３版〉』を完璧にしたうえで、高3の冬から本格的な過去問演習を始めることを目指しましょう。一方で、名古屋大学の場合は東京大学や東京科学大学に近い難易度の問題が出題されることもあります。『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』、『ハイレベル数学Ⅲ・Ｃ［平面上の曲線と複素数平面］の完全攻略〈改訂版〉』まで取り組んだうえで、秋ごろから過去問演習にしっかり時間を割くようにしましょう

共通テストは、大学や学部にもよりますが概ね７割５分〜８割程度の得点が求められます。

秋ごろから、過去問などを用いて本番と同じ制限時間で演習を行いたいです。秋までに、『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 実戦編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 実戦編〈改訂版〉』などの問題集で、共通テストに必要な知識を補い、問題形式に慣れておきましょう。

国公立大学志望のおすすめ数学参考書

旧帝大を除く多くの国公立大学では、入試標準レベルの問題の記述力が求められます。
対策としては、入試標準レベルの問題がバランスよく収録された問題集が効果的です。

国公立大学の標準レベルの問題を多く収録した『国公立標準問題集 CanPass数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］〈第３版〉』『国公立標準問題集 CanPass数学Ⅲ・Ｃ［複素数平面、式と曲線］〈第３版〉』は、解答解説が詳しく記述対策としておすすめです。

また、共通テストは大学や学部学科にもよりますが、およそ6割～7割5分程度が求められます。春休みや夏休みなどの長期休暇を活用し『短期攻略 大学入学共通テスト数学Ⅰ・Ａ 基礎編〈改訂版〉』や『短期攻略 大学入学共通テスト数学Ⅱ・Ｂ・Ｃ 基礎編〈改訂版〉』などの共通テストに必要な知識に絞って効率よく復習できる参考書や問題集を活用し、秋以降の本番形式の演習や模試に備えましょう。

早稲田大学・慶應義塾大学志望のおすすめ数学参考書

早稲田大学、慶應義塾大学の数学は、学部学科によって難易度や出題傾向が大きく異なります。独特な出題も多いので、高3の夏ごろから過去問演習に時間を割きたいです。

文系学部を目指す場合、高2のうちにGMARCH合格レベルを目指して、『数学Ⅰ・A　基本問題演習』『数学Ⅱ・Ｂ・Ｃ［ベクトル］ 基本問題演習』などの数学ⅠAⅡBの入試標準レベルの問題集を終えておくと良いでしょう。高3では、『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』のような入試やや難レベルまで扱っている問題集に取り組みたいです。また、私立大学はマーク式の出題が主ですが、早稲田大学の商学部、社会科学部、慶應義塾大学の経済学部などでは記述式の出題もあります。さらに、早稲田大学の政治経済学部や国際教養学部では、一般入試で共通テスト数学が受験科目になっています。対策が変わってくるので、志望校や学部の受験科目や出題傾向は必ずチェックしておきましょう。

理系学部を目指す場合、早稲田大学・慶應義塾大学ともに東京大学や東京科学大学受験生と同程度の学力が求められます。

高2で『数学Ⅰ・A　基本問題演習』『数学Ⅱ・Ｂ・Ｃ［ベクトル］ 基本問題演習』などの数学ⅠAⅡBの入試標準レベルの問題集を終えておくことに加え、数学Ⅲも網羅系の参考書などに取り組み、入試の基礎となる学習は完了させたいです。高3では、夏までを目安に『ハイレベル数学Ⅰ・Ａ・Ⅱ・Ｂ・Ｃ［ベクトル］の完全攻略〈改訂版〉』『ハイレベル数学Ⅲ・Ｃ［平面上の曲線と複素数平面］の完全攻略〈改訂版〉』といった入試標準～やや難レベルの問題集に取り組みましょう。

理解できるとおもしろい数学の魅力

受験勉強をしていると、数学はミスなく正答にたどり着くことが目的化していくこともあります。しかし、難関大はじめ多くの大学はそれだけではなく、より本質的な思考力を求める出題も少なくありません。

例えば、整数分野の問題は、決まった公式や解法が少なく、自分で仮説を立て検証する力が求められます。実験を通してパターンを見出したり、時には泥臭く数え上げたりして、自分なりの解法を生み出すことが求められるのです。決まったパターンがないので少し不安に感じる人もいるかもしれませんが、自分で考え抜いて正答にたどりつく達成感は、数学の醍醐味と言えるでしょう。

フランスの数学者のポアンカレは、「数学とは、異なるものを同じとみなす技術である」と言いました。例えば、二項定理（二項係数）は最初は数式の展開で学びますが、後に場合の数に深く関連することがわかるでしょう。一見異なる性質の本質を見抜くことが、思考力を育み、入試の難問を解く力につながっていくのです。 そのような思考力を身につけるためにも、良問をたくさん演習することが欠かせません。このコラムを参考に、みなさんに適した参考書・問題集を見つけてみてください。

---